02 Yo-Yo#
Aim#
To show the movement of a yo-yo and the force it exerts on the string that is holding it.
Subjects#
1Q20 (Rotational Energy)
Diagram#

Fig. 203 .#
Equipment#
Yo-yo.
Force sensor.
Data-acquisition system.
Projector to project monitor image.
Presentation#
We all know the yo-yo: Two circular discs with a common shaft and a string several times wrapped around it. Hold the end of the string stationary and release the yo-yo. The string unwinds as the yo-yo drops and rotates with increasing speed. When the unwrapping is completed, the yo-yo climbs again, comes to a stop and starts over again. etc.
Suspending the yo-yo to a force sensor, a registration of the tension in the string is made (red graph in Figure 204 left). When, finally, the yo-yo has come to rest, such a registration is repeated (green line in Figure 204 left).
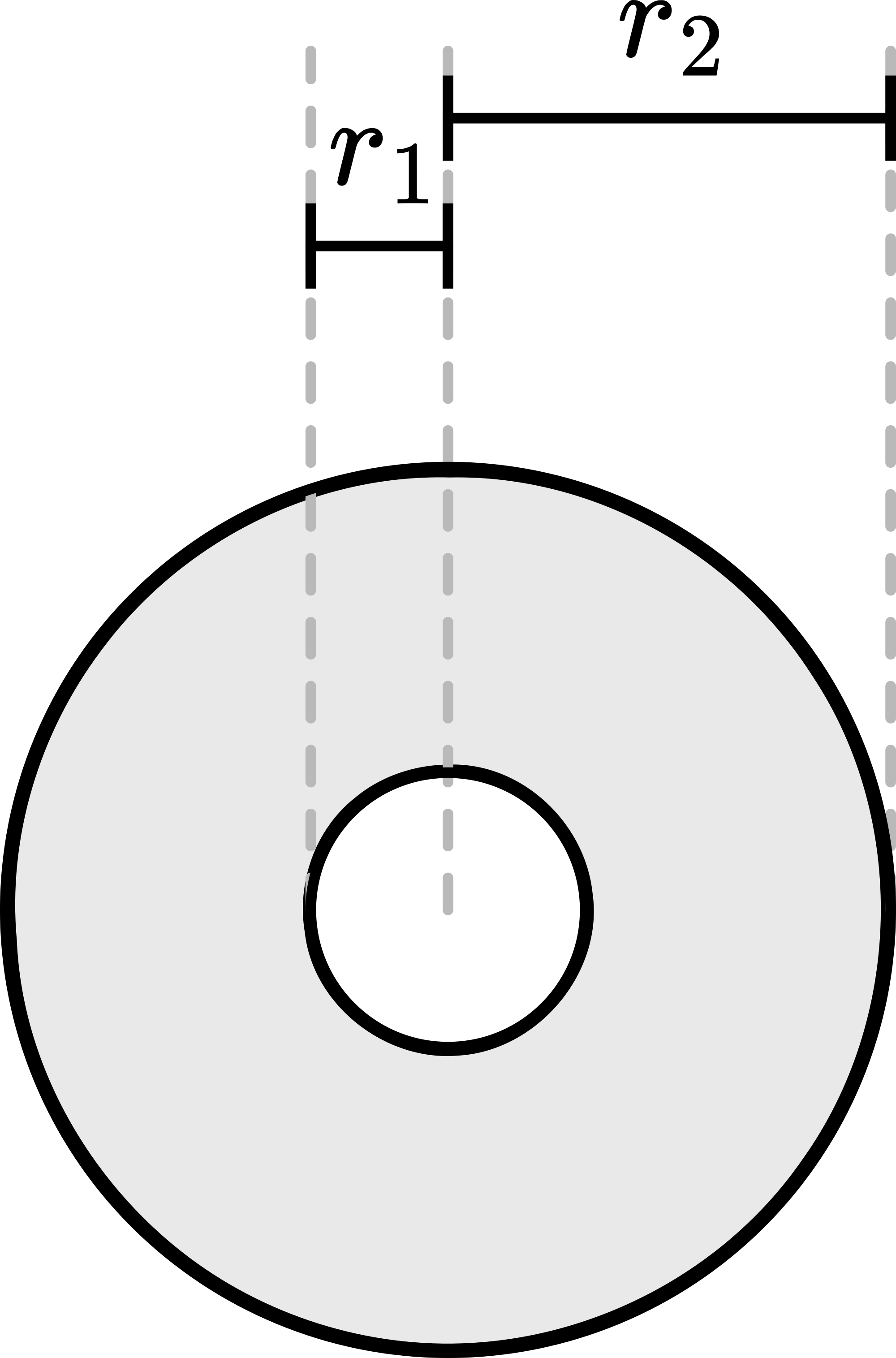
Fig. 204 .#
When studying these graphs, the jerk at the turning point is clearly observed. (Also a strong vibration.) See that the jerk at the turning point is much higher than the weight of the yo-yo.
Going from one jerk to the next, the highest position of the yo-yo is halfway between the two jerks. When a complete cycle is enlarged (see Figure 204 right), it is clear that during the complete cycle the string tension is lower than the weight of the yo-yo.
Explanation#
The yo-yo accelerates (a) due to a force \(m a=m g-F_{s}\left(F_{s}\right.\) being the string tension and \(m\) the mass of the yo-yo.)
When there is no string, then \(F_{s}=0\) and \(a=g\) (free fall);
With a string, \(a\) is always smaller than \(g\) :
\(a=g-\frac{F_{s}}{m}\)
When \(F_{s}\) is just a little smaller than \(m g\), then \(a\) will be very small.
The angular acceleration \((\alpha)\) of the roll during its fall can be found from \(\alpha=\frac{\tau}{I}\), where
the net torque \((\tau)\) is given by \(\tau=m g\).
The acceleration of the center of mass (a) is related to the angular acceleration of the yo-yo by \(a=\alpha r\), so the yo-yo accelerates downward by \(a=\frac{m g r^{2}}{I}\).
Our yo-yo is a simple double disc, so \(I_{C M}=\frac{1}{2} m R^{2}\). It rolls at the circumference of the shaft (radius \(r\) ), that’s why \(I=\frac{1}{2} m R^{2}+m r^{2}\), and we find for the acceleration:
\(a=\frac{2 g}{2+\frac{R^{2}}{r^{2}}}\).
Because \(R>>r, a<<g\).
With our yo-yo we have \(R=150 \mathrm{~mm}\) and \(r=12 \mathrm{~mm}\), so \(a=0.012 \mathrm{~g}\).
Also the string tension can be calculated now: \(F_{s}=m g-m a\), so: \(F_{s}=m g-0.012 m g\), showing that the string tension is just a little lower than the weight of the yo-yo.
Remarks#
A worthwhile observation is, that when the string is unwrapped completely and the yo-yo starts climbing again, that the yo-yo’s translational velocity changes its direction \((-v\) to \(+v)\) but keeps its rotation in the same direction. In other words: its momentum changes direction ( \(-m v\) to \(+m v\) ), but there is no change in angular momentum. The large change of momentum (\(2mv\)) at this point of the yo-yo’s movement explains the jerk (the change of momentum takes place in a very short time).
See also the demonstration Maxwheel in this database in order to link the measured string tension to the acceleration of the yo-yo. Usually we show these two demonstrations together.
Sources#
Borghouts, A.N., Inleiding in de Mechanica, pag. 186-187
Roest, R., Inleiding Mechanica, pag. 183-185
Young, H.D. and Freeman, R.A., University Physics, pag. 303
