01 Self-Inductance in AC Circuit#
Aim#
To show how alternating current depends on the value of self-inductance.
Subjects#
5J10 (Self Inductance) 5L20 (LCR Circuits – AC)
Diagram#

Fig. 521 .#
Equipment#
Lamp, \(220\mathrm{~V}/200\mathrm{~W}\).
Coil, \(\mathrm{n}=500 ; \mathrm{R}=2.5 \Omega\).
U-core with bar.
2 Demonstration meters.
Safety connection box .
Measuring junction box (See Figure 525).
Net-adapter for mobile telephone (or other appliance).
Safety#
It’s a circuit connected to mains voltage (\(220\mathrm{~V}/50\mathrm{~Hz}\)). That’s why we use a safety connection box. This box shows a green light when the mains is disconnected and a red light when the mains is connected. Self-inductance in AC-circuit
Presentation#
The circuit is build as shown in Figure 522 and in Diagram. First we show the circuit setup to the students and then connect the two Voltmeters.
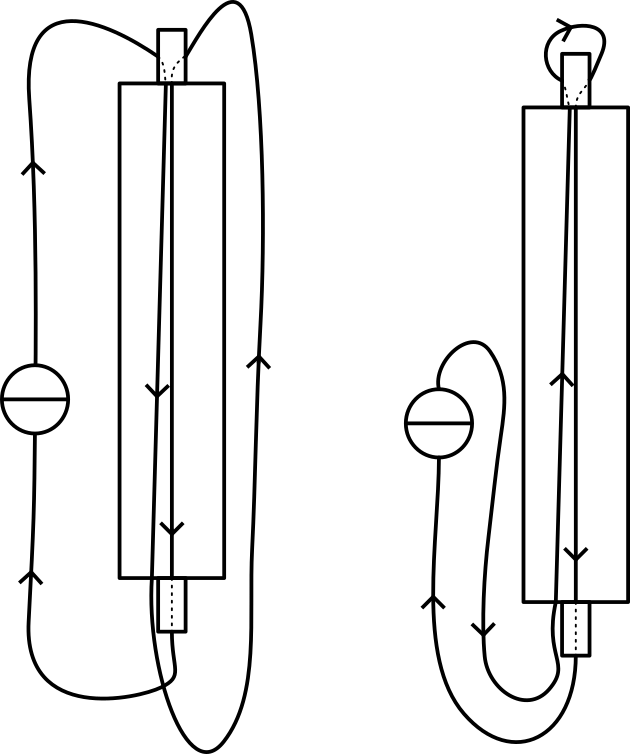
Fig. 522 .#
Connecting the \(220 \mathrm{~V}\) to the circuit makes the lamp glows strongly (see Figure 523A ). The Voltmeter connected to the lamp reads almost \(220 \mathrm{~V}\) : All voltage appears across the lamp; just a very little voltage is read across the coil.
Conclusion is that only a very small emf of self-inductance is generated in the coil.
The bar is partly shifted on to the U-core. As soon as the bar touches the second leg of the \(U\)-core the lamp dims (see figure \(2 B\) ). the Voltmeter across the lamp shows a lower voltage now and at the same time we observe an increase in voltage across the coil.
Conclusion is that there is now a higher emf of self-inductance that opposes the \(220 \mathrm{~V}\).

Fig. 523 .#
When the bar is shifted completely on to the U-core, the lamp only glows very faintly. The voltage read across it is very low. The voltage across the coil is almost \(220 \mathrm{~V}\) now!
Conclusion is that the emf of self-inductance generated in the coil is almost \(220 \mathrm{~V}\) now.
Shifting the bar back and forth across the U-core makes the lamp dim less or more.
Finally we disconnect the lamp. Now only the self-inductance is connected to the \(220 \mathrm{~V}\) (see Figure 524).

Fig. 524 .#
Now the effect of self-inductance is most clear: the voltmeter reads \(220 \mathrm{~V}\) across the coil, and only a small current is flowing (we measure \(0.4 \mathrm{~A}\) ). When there would be no self-inductance, the current would be \(220 \mathrm{~V} / 2.5 \Omega=88 \mathrm{~A}\) !
Conclusion is that the emf of self-inductance really opposes the applied voltage. 5. The same demonstration is performed with a commercial net-adapter (used as charger for a mobile telephone; see Figure 525). Here also only the primary coil of the adapter is connected to the mains. We read a current of only \(0.3 \mathrm{~mA}\)!

Fig. 525 .#
Explanation#
The emf induced in a coil is, from Faraday’s law: \(E=-N \frac{d \Phi_{B}}{d t}=-L \frac{d I}{d t} ; L\) being the coefficient of self-inductance. For a solenoid with a core \(\left(\mu_{r}\right)\) this is:
\(L=\frac{\mu_{r} \mu_{0} N^{2} A}{l} L=\frac{\mu_{r} \mu_{0} N^{2} A}{l}\). This shows that the higher \(L\), the higher the emf of self-inductance. Shifting the bar across the core changes \(L\), and so the induced emf.
Remarks#
The core on the bar makes a lot of noise. This is a \(100 \mathrm{~Hz}\) mains hum due to the mains frequency \((50 \mathrm{~Hz})\).
The effect of self-inductance can also be translated into impedance of the circuit. In our demonstration 4. the circuit shows an impedance of \(220 \mathrm{~V} / 0.4 \mathrm{~A}=550 \Omega\) instead of the \(2.5 \Omega\) of the copper coil.
In figure B we read \(V_{\text {coil }}=130 \mathrm{~V}\) and \(V_{\text {lamp }}=110 \mathrm{~V}\). Students easily read this as a total of \(240 \mathrm{~V}\), so higher than the applied \(220 \mathrm{~V}\). Phase-shift between these two voltages is responsible for that. The situation must be something like Figure 526 below shows.
Fig. 526 .#
Video Rhett Allain#
Sources#
Giancoli, D.G., Physics for scientists and engineers with modern physics, pag. 758-759 and 773-774.
Wolfson, R., Essential University Physics, pag. 474-477 and 491-492. 110V
