05 Coriolis (3)#
Aim#
To elucidate the direction of the Coriolis force on our rotating Earth.
Subjects#
1E20 (Rotating Reference Frames)
1E30 (Coriolis Effect)
Diagram#
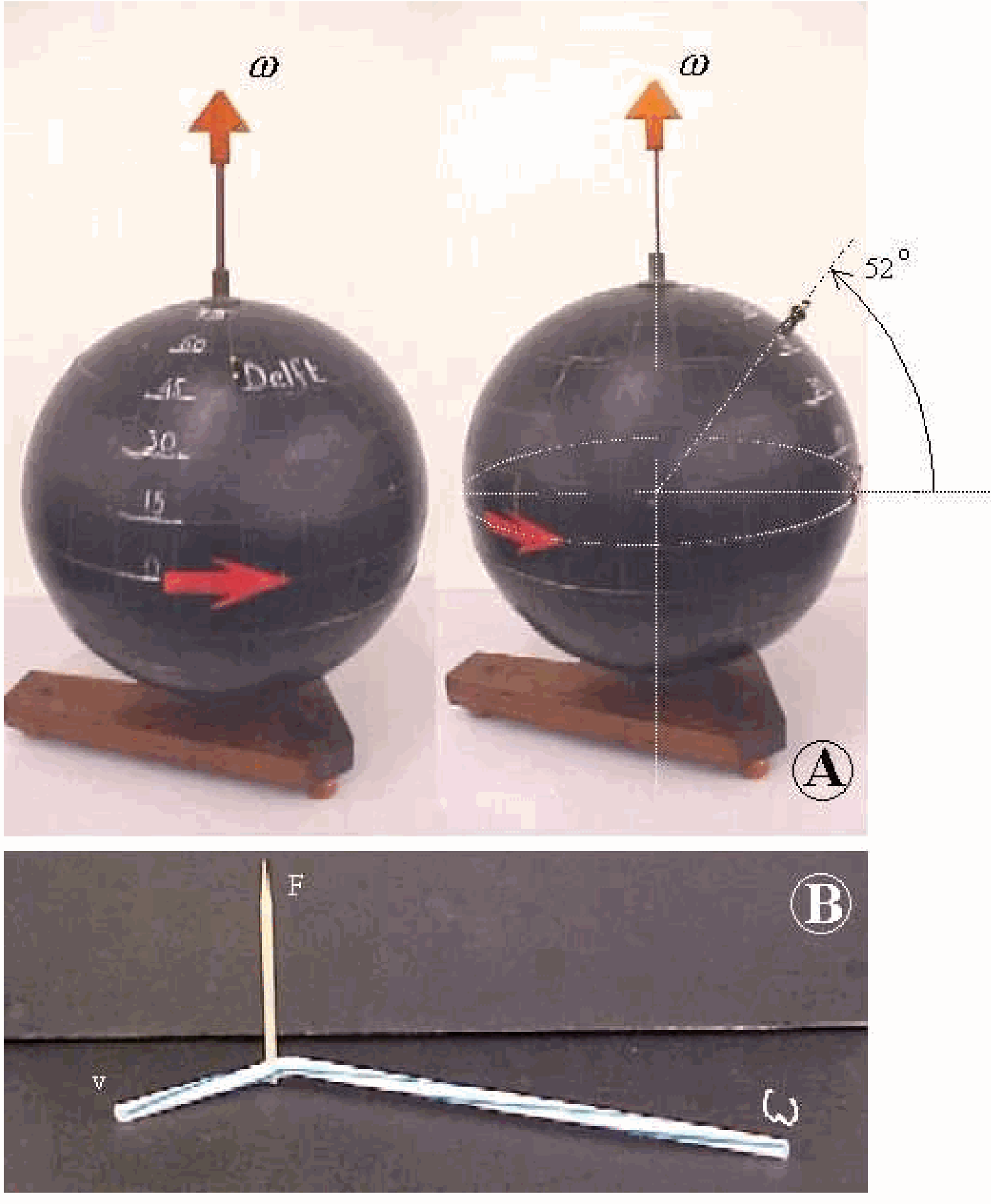
Fig. 61 .#
Equipment#
Globe.
Flexible straw (\(v\) and \(\omega\) in Diagram B).
Toothpick (\(F\) in Diagram B).
Presentation#
On the globe, our local position is indicated by sticking a small puppet at our coordinates (Delft, \(52^{\circ}\) northern latitude; see Diagram A). On the globe, the sense of rotation is indicated by arrows stuck to the equator. This sense of rotation is also marked by the \(\omega_{0}\)-vector stuck into the North Pole.
The flexible straw is used as a resource to indicate simultaneously the direction of \(\omega_{0}\) and the direction in which an object is moving (velocity \(v\) ). The long arm of the straw is used to indicate the direction of \(\omega_{0}\), and the short arm is used to indicate the direction of \(v\). Applying the corkscrew rule ( \(\vec{F}_{\text {cor }}=-2 m(\vec{\omega} \times \vec{v})\) ), the direction of \(F_{\text {cor }}\) is indicated by sticking the toothpick into the elbow of the flexible straw (see Diagram). The advantage of using the flexible straw is that easily the angle between \(\omega_{o}\) and \(v\) can be changed; the toothpick can be easily shifted in and out the elbow when the corkscrew rule indicates that the direction of \(F_{\text {cor }}\) is different (see Figure 62).
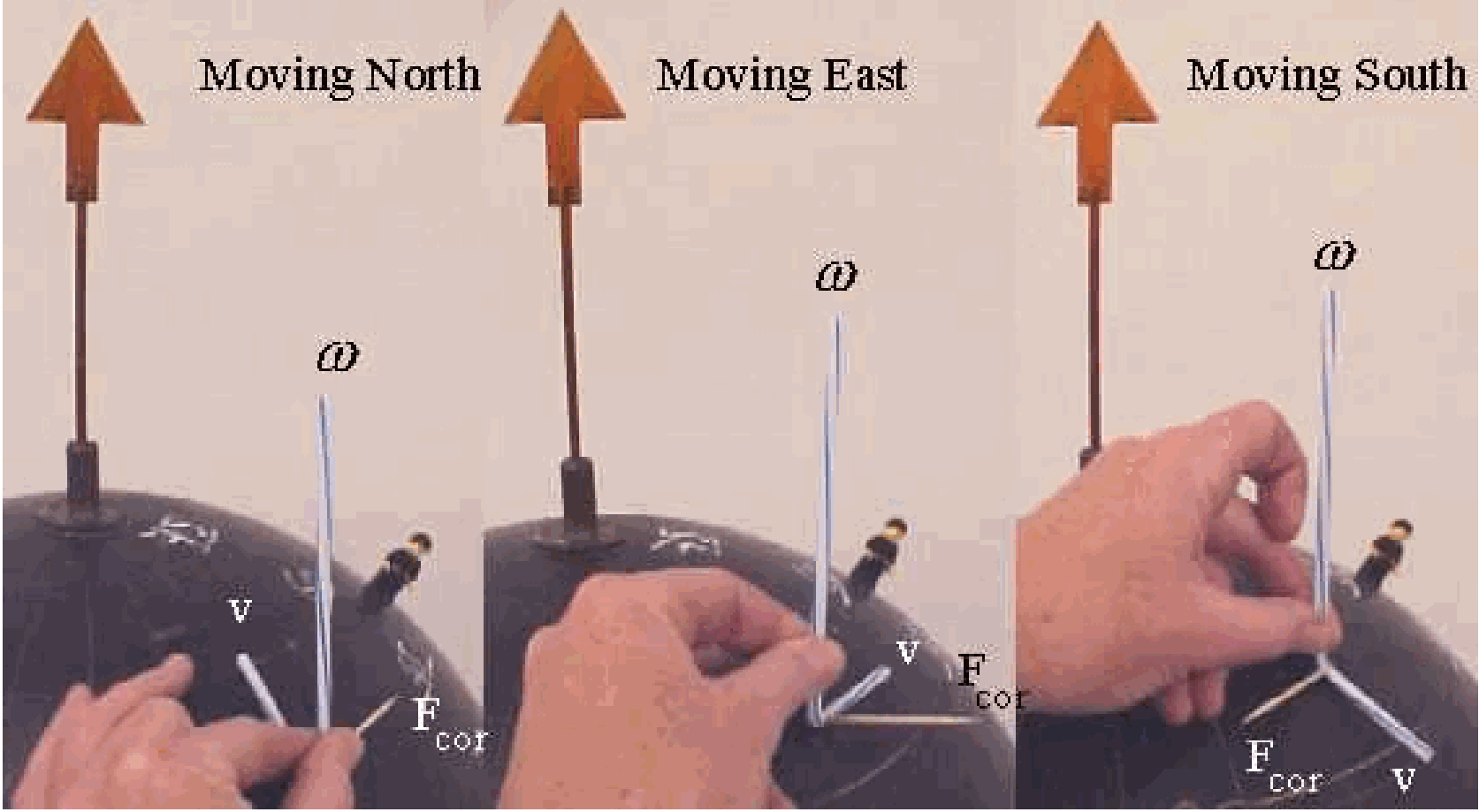
Fig. 62 .#
Remarks#
On the Southern hemisphere, this straw-toothpick vector model can be used when you keep \(\omega_{0}\) pointing upwards, meaning that you have to keep the model a distance away from the globe.
Sources#
Mansfield, M and O’Sullivan, C., Understanding physics, pag. 182
McComb,W.D., Dynamics and Relativity, pag. 137-145
Roest, R., Inleiding Mechanica, pag. 197-202; 205-210
Giancoli, D.G., Physics for scientists and engineers with modern physics, pag. 291-292
