03 Maxwheel

03 Maxwheel#

Aim#

  • To show the conversion of potential energy into rotational kinetic energy and vice-versa.

  • To show the effect of a large moment of inertia.

Subjects#

  • 1Q20 (Rotational Energy)

Diagram#

../../../../../_images/figure_088.png

Fig. 202 .#

Equipment#

  • Wheel of Maxwell.

  • Motion sensor.

  • Data-acquisition system.

  • Projector, to project monitor-image.

  • Overheadsheet with the dimensions of the wheel.

Presentation#

The wheel is rolled by hand to its uppermost position. When released, the wheel moves downward slowly and starts rotating. In its lowest position, the speed of rotation is maximum and the wheel rolls upward again, almost reaching the starting position. This pattern repeats itself.

Going through its lowest position, a strong jerk can be observed.

Using a motionsensor, placed under the wheel (see Diagram), the position of the wheel can be measured continuously using a data-acquisition system. Such a system enables to calculate velocity and acceleration and display these variables graphically while the wheel is running up and down (see Figure 203). After a couple of periods data-acquisition is stopped and the results can be discussed:

From the position-graph (see Figure 203) we read \(\Delta h=0.7 m\), giving that \(E_{\text {pot }}\) changes an amount \(\Delta E_{\text {pot }}=m g \Delta h=m g \cdot 0 .7\), so around \(7 \mathrm{~m}[\mathrm{~J}]\).

../../../../../_images/figure_166.png

Fig. 203 .#

Out of the velocity graph, at the end of the descent we read that the absolute value of the velocity is around \(0.25 \mathrm{~m} / \mathrm{s}\). So \(E_{\text {trans }}=1 / 2 m v^{2}\), so around \(0.03 \mathrm{~m}[\mathrm{~J}]\) !.

These numbers show that in this demonstration only a very small part \((1 / 244)\) of the potential energy appears as translational kinetic energy. The rest will appear as rotational kinetic energy; almost all the energy is transformed into the rotation of the wheel.

Part of the graph of the acceleration is magnified in order to read the value of the acceleration. Also this experimental value can be checked by calculation (see Explanation).

Explanation#

While moving downwards, a large portion of the potential energy is converted into rotational kinetic energy rather than into translational kinetic energy.

\(\Delta E_{\text {pot }}=E_{\text {trans }}+E_{\text {rot }}\), so

\(m g h=\frac{1}{2} m v^{2}+\frac{1}{2} I \omega^{2}\), with \(\omega=\frac{v}{r_{1}}\) and \(I=m\left(R^{2}+r_{1}^{2}\right)\).

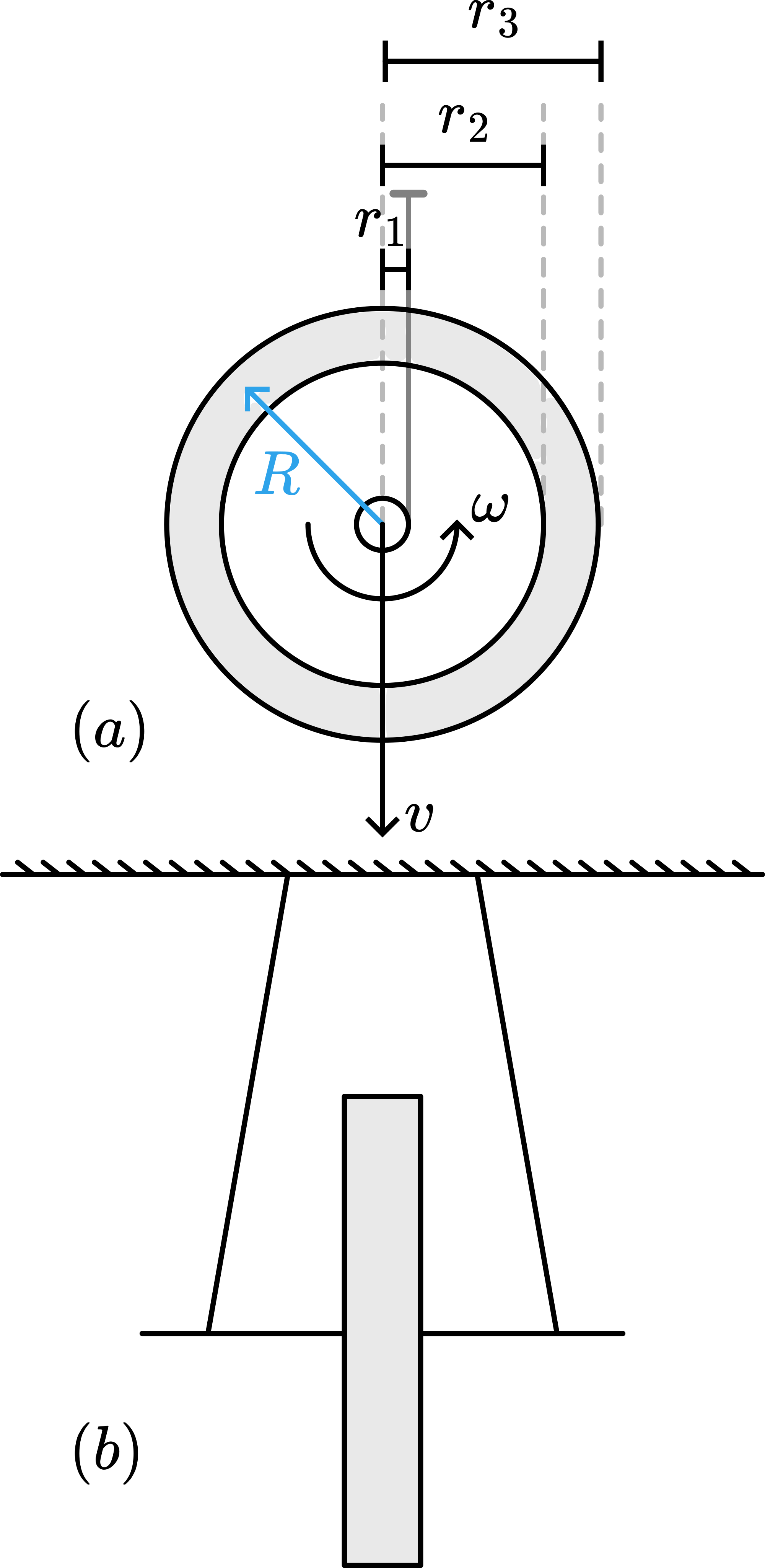
../../../../../_images/figure_228.png

Fig. 204 .#

We find:

\[ E_{\text {pot }}=\frac{1}{2} m v^{2}+\frac{1}{2} m\left(\frac{R^{2}}{r^{2}}+1\right) v^{2} \]

In our demonstration \(r_{1}=3.5 \mathrm{~mm}\) and \(\mathrm{R}=57 \mathrm{~mm}\), and so we have.

\[ E_{p o t}=\frac{1}{2} m v^{2}+266 \frac{1}{2} m v^{2} \]

We see that only a very small amount of the potential energy is converted into translation, the difference being indicated by the factor 266 . The translational acceleration will be a factor 267 times smaller than \(g\). This statement is confirmed by the acceleration-graph (see magnified part to read a significant value).

(For a quick calculation we use \(R=50 \mathrm{~mm}\) and \(r=3.5 \mathrm{~mm}\), giving \(R^{2} / r^{2}=200\).)

Passing through its lowest point, the wheel changes its momentum from \(-m v\) to \(+m v\) (total change of \(2 m v\) ). Quite a large force \(F\) is needed for this because the time \(\Delta t\) in which the change in momentum takes place is small. The impulse \(F \Delta t\) is delivered by the threads in which, during half a period of rotation, a higher tension occurs.

Remarks#

  • Care must be exercised so that the two threads always have the same length and so there is no overlapping on the spindle which would change \(r_{1}\). In our wheel, overlapping is prevented by giving different lengths to the spindle and suspension bar (see Figure 204B).

  • When measuring \(r_{1}\) do not forget the thickness of the thread!

  • As an introduction to this experiment see the demonstration “Yo-yo” in this database. Doing so, the measured acceleration can be related to the force of the strings holding the wheel.

Sources#

  • Meiners, Harry F., Physics demonstration experiments, part I, pag. 286

  • Friedrich, Artur, Handbuch der experimentellen Schulphysik, part 2, Mechanik der festen Körper, pag. 214

  • Roest, R., Inleiding Mechanica, pag. 183-185

  • Young, H.D. and Freeman, R.A., University Physics, pag. 303

Contents