02 Galilean Cart#
Aim#
To show and discuss an example of Galilean transformations
Subjects#
1E10 (Moving Reference Frames)
Diagram#

Fig. 35 .#
Equipment#
Two carts, easy rolling and able to carry a human being; construction as shown in the diagram.
Large funnel (outlet reduced to \(4 \mathrm{~mm}\)), suspended by three cords.
Clamping material to support the funnel-pendulum.
\(1 \mathrm{~kg}\) of salt.
Broom.
Presentation#
One person sits on the cart, fills the funnel with salt while keeping the outlet closed with a finger, and then gives the funnel pendulum a deflection in the \(x'\)-direction. The demonstrator moves the cart with constant speed along the front of the lecture hall (\(y\)-direction). As soon as the cart moves at a constant speed, the person on the cart sets the pendulum swinging. A salt track is left on the floor of the lecture hall (see Figure 37). This track records the motion of the swinging funnel in the \(x\)-\(y\) plane.
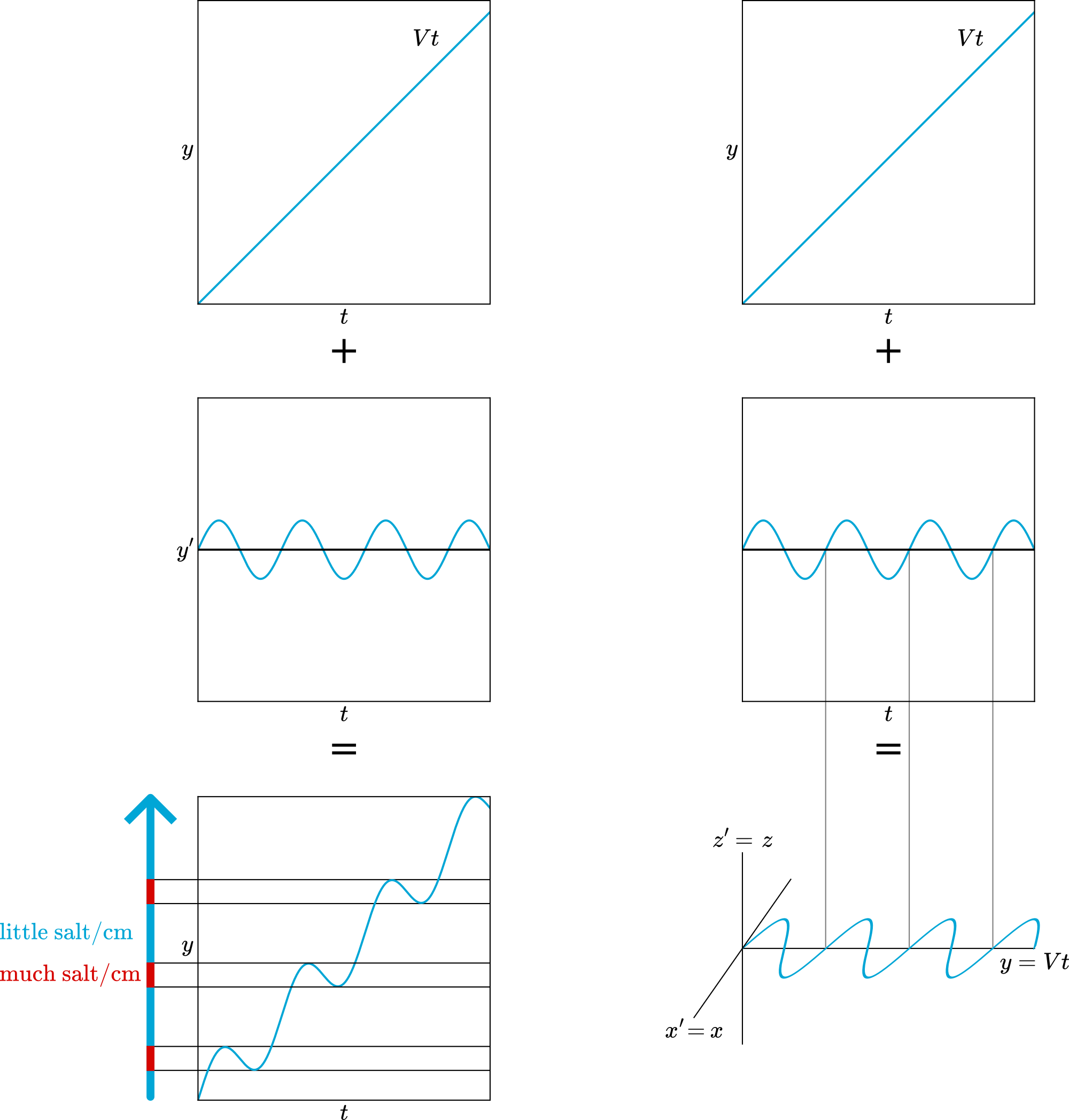
Fig. 36 .#
The same demonstration is performed, but now with the funnel-pendulum swinging into the \(y'\)-direction. A second salt-track appears on the floor (see Figure 36).
Again, the salt track shows the recording of the movement of the swinging funnel in the \(x\)-\(y\) plane.
The results are discussed.
Explanation#
The pendulum moves in the \(x^{'}\)-\(y^{'}\)-\(z^{'}\)-frame according to: \(x^{'}=A \sin (\omega t+\phi)\); \(y^{'}=0 ; z^{'}=0\). The writing on the ground in salt is in the \(x-y-z\)-frame. The \(x^{'}-y^{'}-z^{'}-\) frame moves with a speed \(\mathrm{V}\) into the \(\mathrm{y}\)-direction., so a point measured in the \(x^{'}-\) \(y^{'}-z^{'}\)-frame will have an \(y\)-coordinate: \(y=V t\). (see Figure2).
When the pendulum swings into the \(y^{'}\)-direction, the movements in the \(x\)-y-zframe will be: \(y=V t+A \sin (\omega t+\phi) ; x=0\) and \(z=0\) (see Figure 37).

Fig. 37 .#
Remarks#
As Figure 36 makes clear, the difference between much - and little salt is more pronounced when \(y=V t\) is steeper; that is at higher speeds of the cart.
Sources#
Mansfield, M and O’Sullivan, C., Understanding physics, pag. 173-174
McComb,W.D., Dynamics and Relativity, pag. 24-25
