03 Boomerang Ball (2)#
Aim#
The concept of impulse explains this very peculiar behavior of a bouncing ball.
Subjects#
1K10 (Dynamic Torque)
1N10 (Impulse and Thrust)
Diagram#

Fig. 103 .#
Equipment#
Superball.
Table.
Safety#
A superball can jump into many unexpected directions, so mind vulnerable objects in the neighborhood.
Presentation#
The table is positioned as shown in Diagram. The ball is thrown as shown. The ball bounces to a fro.
Explanation#
As a basis to explanation see the demonstration Boomerang ball. Using a large basketball thrown against the floor and then bouncing against a vertical wall, shows that after hitting the vertical wall the basketball still rotates clockwise. Figure 104A shows this.
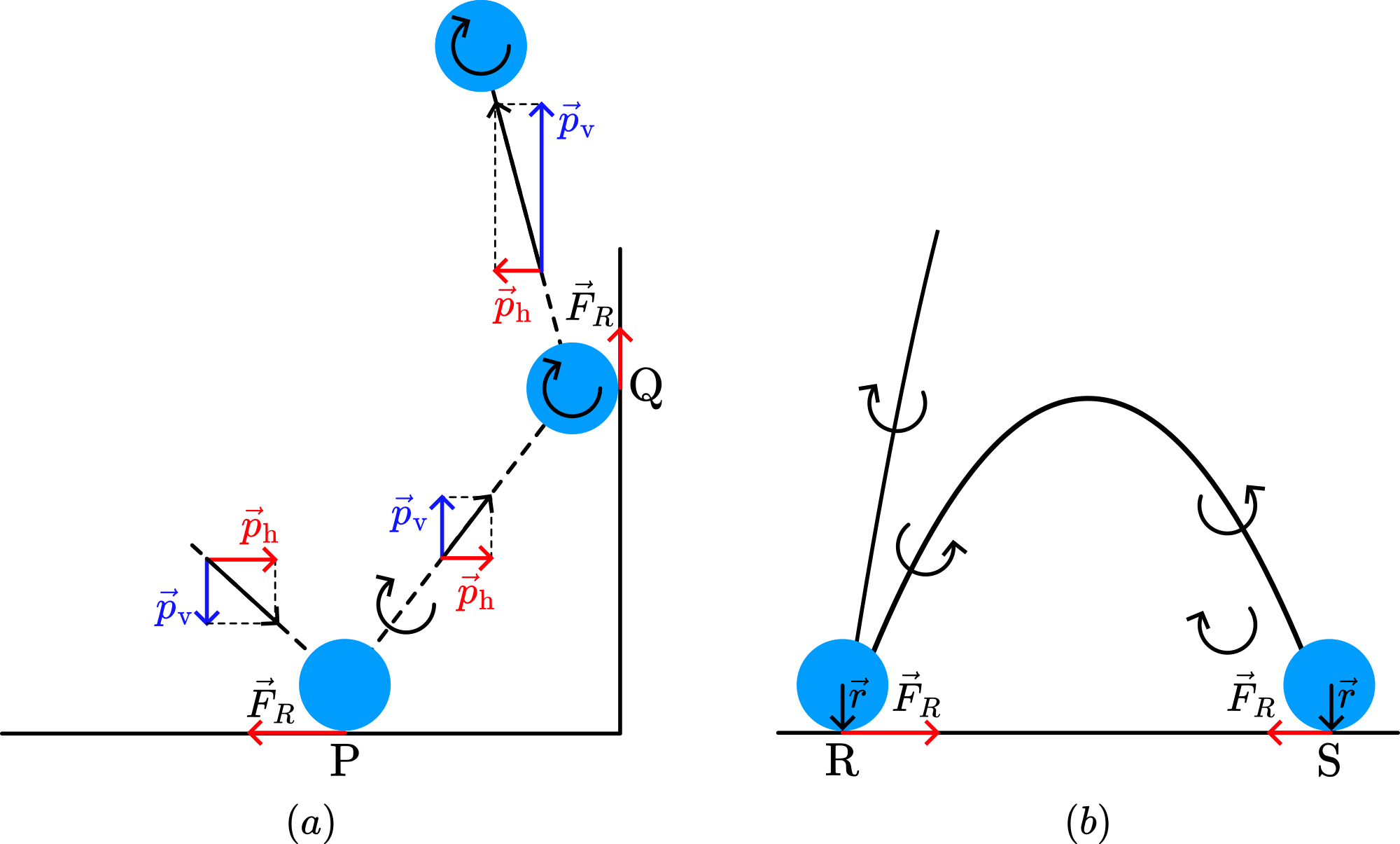
Fig. 104 .#
(The effect of the friction force \(F_{R}\) in \(\mathrm{Q}\) is not that large as that of \(F_{R}\) in \(\mathrm{P}\), since the ball approaches the vertical wall with \(\vec{p}_{h}\) and this momentum is smaller than
\(\vec{p}_{v}\) in P.)
Having hit the vertical wall the ball climbs steep (see Figure 104A). A parabolic trajectory follows. On hitting the floor in \(\mathrm{R}\), the friction force is directed to the right (Figure 104B). The impulse \(\int F_{r} d t\) is large enough to make the component
\(\vec{p}_{h}\) change direction and \(\bar{M}=\vec{r} \times \vec{F}_{R}\) is inducing a counter clockwise rotation. It bounces towards \(\mathrm{S}\) and again \(F_{R}\) is directed to the inner side of the parabola, making the component \(\vec{p}_{h}\) reverse direction and \(\bar{M}=\vec{r} \times \vec{F}_{R}\) inducing clockwise rotation. And so on.
Remarks#
Practicing this demonstration against a real wall will learn that this part of the demonstration can also be appreciated on its own. Having the right speed and right angle, a very high climbing ball will be the result of your practicing. Figure 104A shows the explanation of this phenomenon: After bouncing at \(\mathrm{Q}\), \(\vec{p}_{v}\) has a very high value.
A nice variation to this demonstration is the “drunken student” (sorry, “drunken sailor”). To throw a ball that follows such a staggering trajectory, see Figure 105.
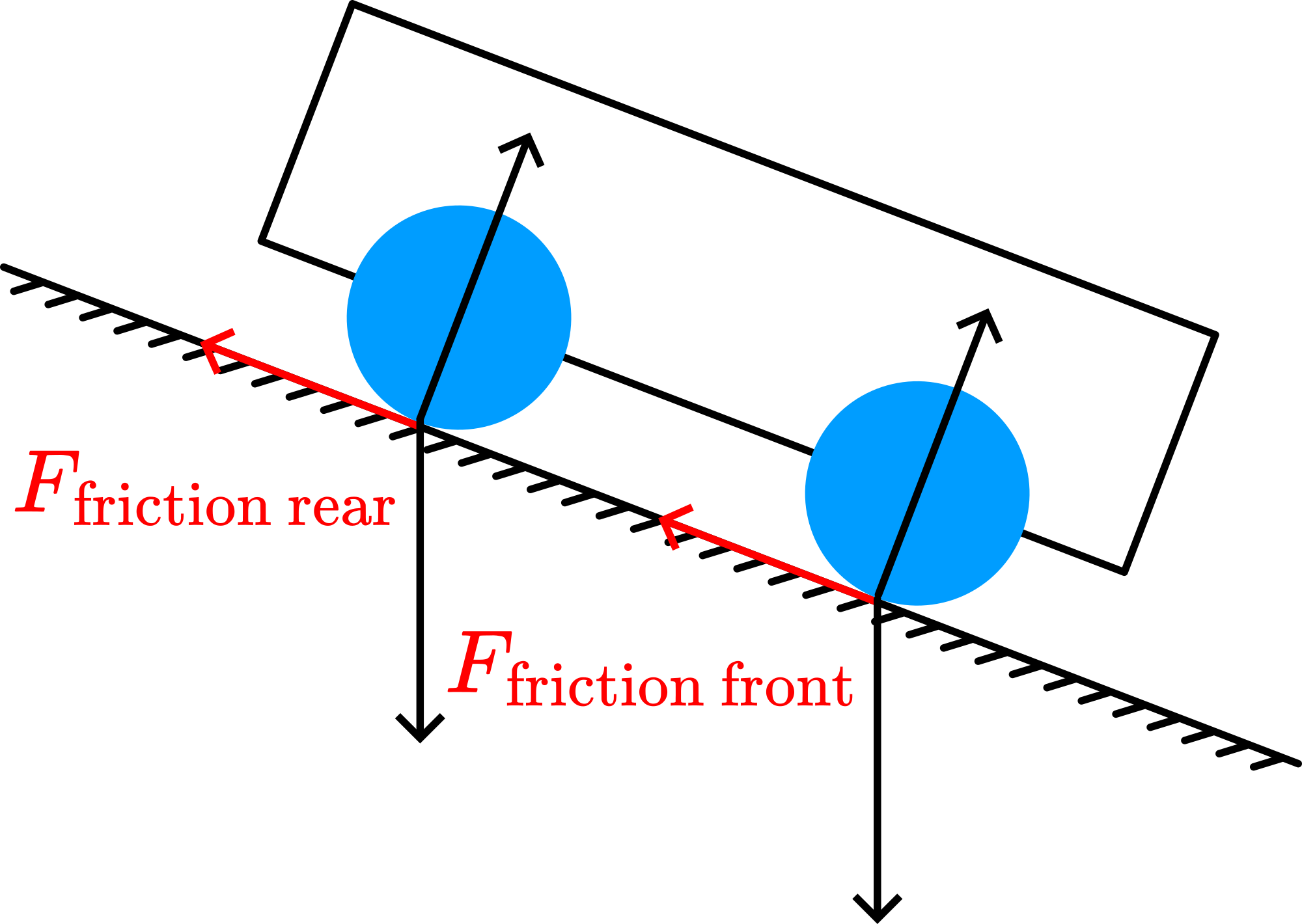
Fig. 105 .#
Sources#
Walker, J., Roundabout, the Physics of Rotation in the Everyday World, pag. 8-12.
American Journal of Physics, pag. 875-883 (Vol. 72-7; 2004).
