01 Going Round in Circles

01 Going Round in Circles#

Aim#

To see/feel the centripetal force.

Subjects#

1D50 Central Forces

Diagram#

../../../../../_images/figure_04.png — Fig. 21 .#

Equipment#

Tube, with rounded edges, $l=15 \mathrm{~cm}$.
Piece of rope, $l=1.5 \mathrm{~m}$.
Two rubber stoppers $\left(m_{1}\right)$.
A number of weights $\left(m_{2}\right)$. We use thick washers.
Paperclip.
(Stopwatch).

Presentation#

The diagram shows the components and how to use them. By swinging the tube slightly, the mass $m_{1}$ begins to move in circles above your head. The demonstrator must swing $m_{1}$ at a specific frequency to balance the system.

../../../../../_images/figure_14.png — Fig. 22 .#

When the demonstrator slows down to a lower frequency, $m_2$ moves downward, causing $m_1$’s circular path to become smaller and smaller. Speeding up causes $m_2$ to rise, and $$m_1$$ moves in increasingly larger circles.
The demonstrator first swings $m_1$ in a stable circular motion. Then, by pulling $m_2$ downward, $ m_1$ speeds up dramatically, tracing tighter and tighter circles.

If time permits, the relationship between the variables in this demonstration can be verified more exactly. Just below the tubing, a paperclip is fixed to the rope used as a marker to make $m_{1}$ go round in a circle with fixed $R$. A stopwatch can be used to time the frequency.

When $m_1$ is doubled by adding another rubber stopper to it, a lower frequency is needed to balance the system.
When $m_{2}$ is increased, a higher frequency is needed to balance the system.
When half the rope length is used (shifting the paperclip), a higher frequency is needed to balance the system.

Explanation#

Analysis shows that movement at a constant speed ( $v$ ) of a mass ( $m_{1}$ ) in a circle with radius $R$ can be described by $a_{c}=\frac{v^{2}}{r} \omega^{2} R$. In our demonstration the tension ( $T$ ) in the string provides the force needed for $a_{c}: T=m_{1} a_{c}$, and $m_{2} g=m_{1} a_{c} \Rightarrow a_{c}=\frac{m_{2}}{m_{1}} g$, (see Figure 23).

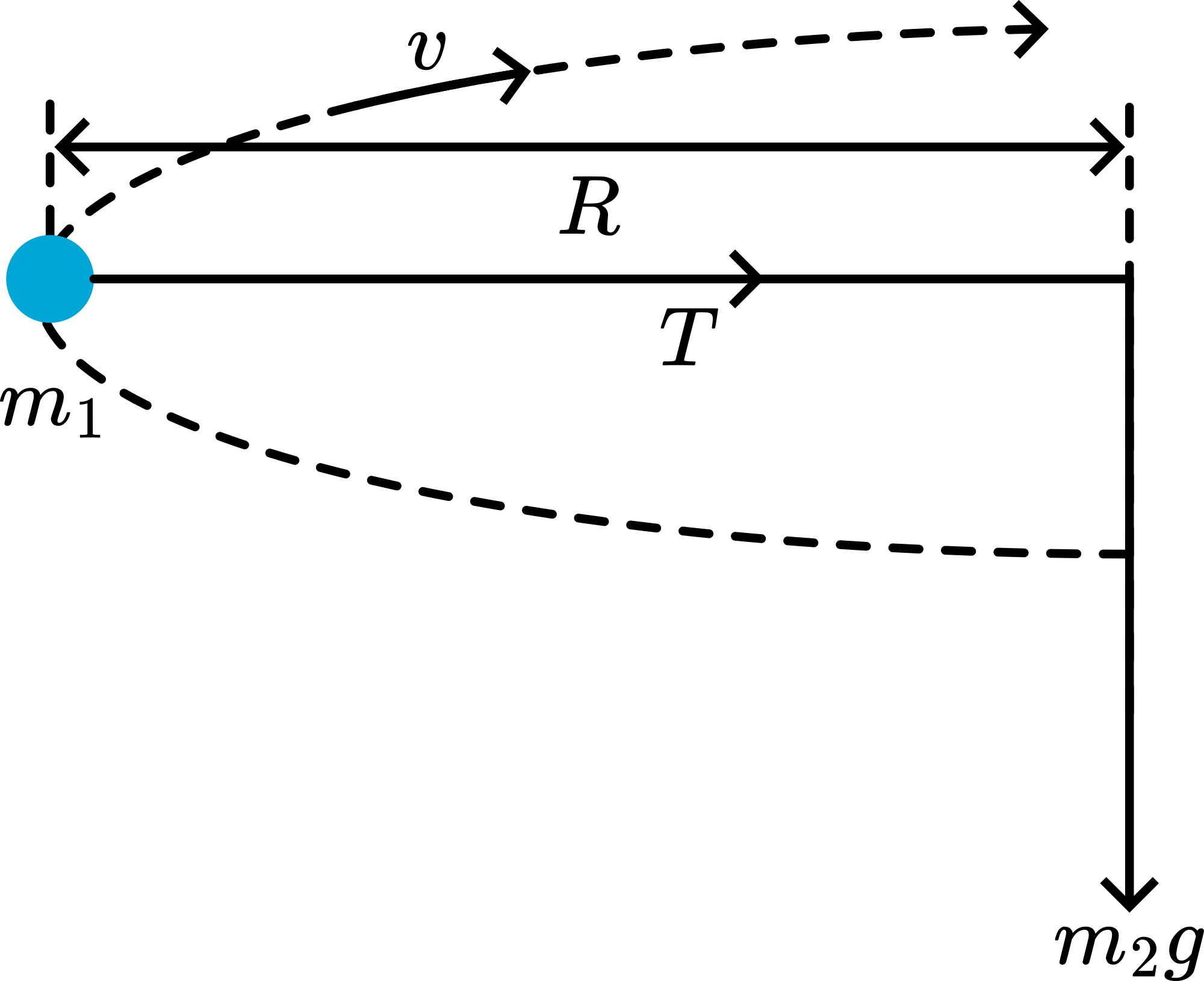
../../../../../_images/figure_22.png — Fig. 23 .#

First, the demonstrator showed a balanced situation, after which he slowed down $\omega$. The centripetal acceleration, describing such a slower movement, will be lower $\left(a_{c}=\omega^{2} R\right)$. But $T$ is a fixed value, so $T$ will pull $m_{1}$ inwardly. As $a_{c}=\omega^{2} R$ shows, this proces is cumulative and $m_{1}$ ends at the centre of the circle.
When $m_2$ is pulled downward, the string tension increases substantially, and so does $a_c$. According to $a_c = \omega^2 R$, and given that $R$ decreases, $\omega$ increases significantly.

Doubling $m_1$ means that the centripetal acceleration $a_c$ provided by the string tension will be halved $\left(a_c = \frac{m_2}{m_1} g\right)$. To keep $m_1$ moving in the same circle, $\omega$ must decrease by a factor of $\sqrt{2}$ according to $\left(a_c = \omega^2 R\right)$.
Increasing $m_2$ raises the string tension, so the provided $a_c$ increases $\left(T = m_1 a_c\right)$. To keep $m_1$ moving in the same circle, $\omega$ has to increase.
When $R$ is halved but the tension in the string remains the same, the provided $a_c$ also remains constant. To keep $m_1$ moving in a (smaller) circle, $\omega$ must increase by a factor of $\sqrt{2}$ according to $\left(a_c = \omega^2 R\right)$.

Remarks#

Practice the demonstration before you show it. A practiced hand is needed to make $m_1$ go round properly.
Rubber stoppers are used as masses moving in circles for safety reasons.
The spinning mass should be light compared to the hanging weight (about a factor of 3), because otherwise the angle between the string and the vertical will not approach $90^\circ$. This leads to more friction, and due to the slanting rope (forming a cone around the circle), the analysis changes.
In the last part of the presentation (grabbing and pulling $m_2$ downward), the demonstrator will feel that quite a lot of force is needed. It is, of course, most instructive for the students if they experience this force themselves (perhaps during the coffee break?).

Sources#

Ehrlich, Robert, Turning the World Inside Out and 174 Other Simple Physics Demonstrations, pag. 72-73
Mansfield, M and O’Sullivan, C., Understanding physics, pag. 68-71 and74-75