03 Pulling a Thread

03 Pulling a Thread#

Aim#

To use Newton’s second law to explain a surprising demonstration.

Subjects#

  • 1G10 (Force, Mass, and Acceleration)

Diagram#

../../../../../_images/figure_026.png

Fig. 75 .#

Equipment#

  • Mass of \(5 \mathrm{~kg}\).

  • 4 identical masses, \(1 \mathrm{~kg}\) each (see Remarks).

  • Thin cotton thread.

  • A bar to hang the masses.

Safety#

  • Mind the falling weights! You can put a foam cushion under the weights.

Presentation#

  1. The mass of \(5 \mathrm{~kg}\) is suspended by a strong thread. Through a thin cotton thread, it can be displaced horizontally by slowly pulling on this thread. However, when a quick jerk is given, the thin cotton thread breaks.

  2. Using a thin thread, the two masses of \(1 \mathrm{~kg}\) are hung on to the bar. On the bottom side of each mass, a free-hanging thread is tied. Ask the students which thread will break, the upper or the lower, when we slowly increase the pulling force on the bottom thread. Slowly pull the lower thread of one mass. This will cause the upper thread to break. Then ask the students which thread will break when we increase the pulling force on the lower thread very fast. Pull the lower thread on the second mass rapidly. This time, the lower thread will break.

Explanation#

  1. The tension ( \(T\) ) in the thin thread equals the force applied to the thread: \(F=T\). This force accelerates \(m\) (see Figure 76). A jerk means that \(a\) is high; a high \(F(=m a)\) is needed for that. The tension in the thread will be high, resulting in the breaking of this thread.

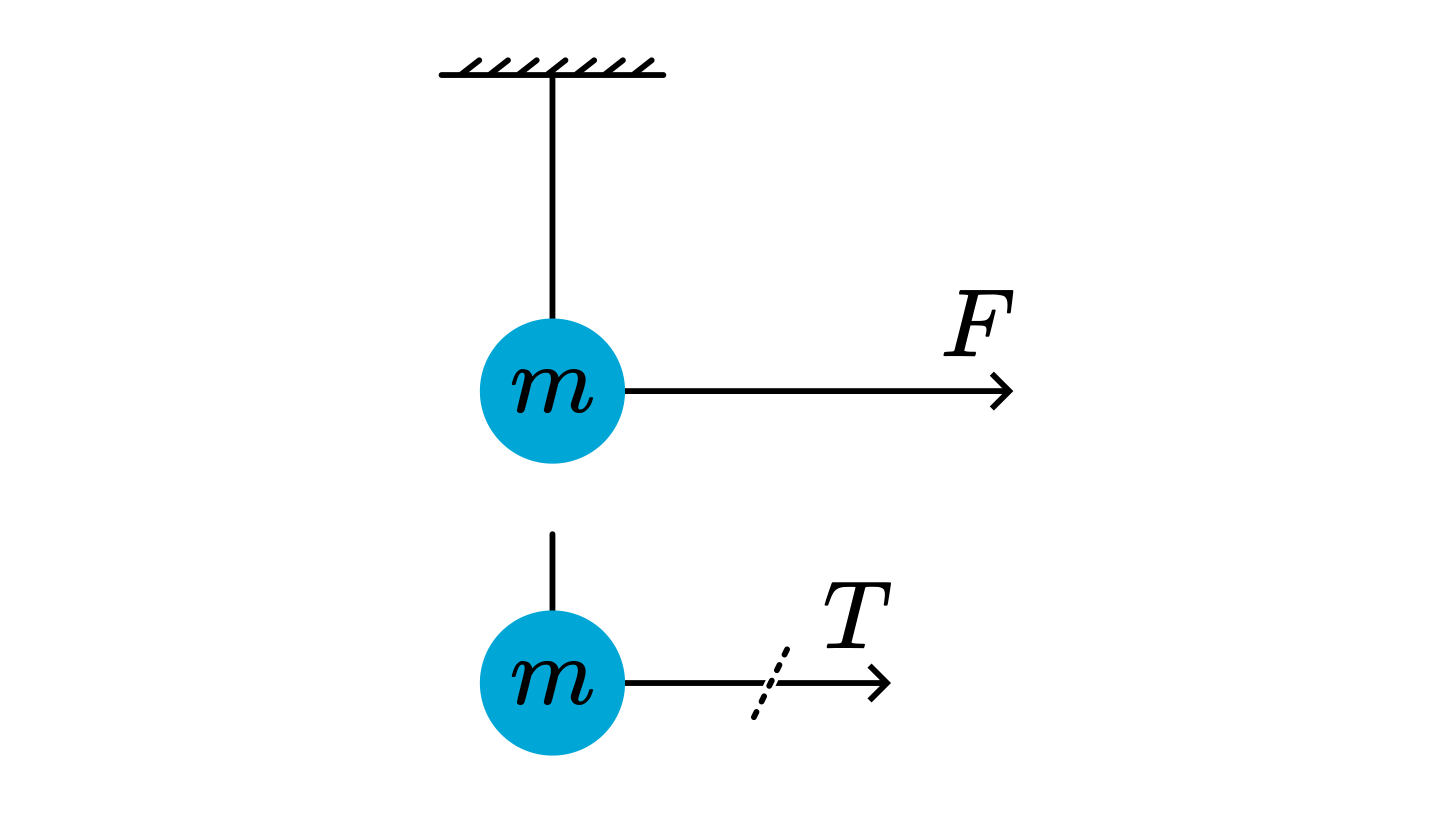
../../../../../_images/figure_120.png

Fig. 76 .#

a. A general explanation When we increase the pulling force slowly, a low acceleration \(a\) is imparted to the mass. The mass can follow this acceleration, causing a stretch in the upper thread. The upper thread also supports the weight of the mass, so it is the thread that eventually breaks. However, when we try to give the mass a high acceleration suddenly, the inertia of the mass prevents it from following the motion of our hand quickly; it lags. As a result, the thread between our hand and the mass experiences a large stretch and breaks. Meanwhile, the upper thread remains unaffected because the mass is no longer moving downwards; it only supports the weight of the mass, as it did before.

*b. An analytical explanation* Using Newton's second law gives still more insight. The forces acting on $m$ are $T_{1}, T_{2}$ and $m g$ (see {numref}`Figure {number} <1g1003/figure_2.png>`). $T_{1}$ is the tension in the upper thread. The tension in the lower thread is $T_{2}$. The acceleration $a$ that $m$ obtains can be determined by: $m a=T_{2}+m g-T_{1}$

It follows: $m a-m g=T_{2}-T_{1}$ or $m(a-g)=T_{2}-T_{1}$
../../../../../_images/figure_210.png

Fig. 77 .#

As long as \(a<g\), then \(T_{2}<T_{1}\) and the top-thread will break. But when \(a>g\), then \(T_{2}>T_{1}\) and the bottom-thread will break.

This last explanation shows the power of Newton’s second law: now it is possible to say something about the acceleration \(a\), which determines what will happen (i.e., which thread will break).

(A student asked: what will happen when \( a = g \)?)

Remarks#

  • We suspend 4 masses to perform the demonstration twice (without tedious knotting).

  • Presentation 1 can be directly referred to the common experience that when pulling a damaged car by another car, the pulling car should start slowly, otherwise the pulling rope will break.

  • A variation to presentation 1 is attaching a thread to a mass and slowly pulling upward, lifting the mass. Repeating this with a jerk will break the thread.

  • In a more sophisticated analysis, also the elasticity and length of both cords should be taken into account (see AJP- and PT-articles mentioned in Remarks).

Video Rhett Allain#

Sources#

  • Ehrlich, Robert, Turning the World Inside Out and 174 Other Simple Physics Demonstrations, pag. 30.

  • Friedrich, Artur, Handbuch der experimentellen Schulphysik, part 2, Mechanik der festen Körper, pag. 85.

  • Freier, George D. and Anderson, Frances J., A demonstration handbook for physics, pag. M16.

  • Sutton, Richard Manliffe, Demonstration experiments in Physics, pag. 46-47.

  • American Journal of Physics, pag. 860-862 (Vol. 72-7; 2004).

  • The Physics Teacher, pag.504-507 (Vol. 34; Nov. 1996).

Contents