05 Percussionpoint (2)#
Aim#
To show what any batter can tell you: if you hit the ball at a certain point, there will be no impulse transferred to your hands (the batter experiences no “sting”).
Subjects#
1Q60 (Rotational Stability)
Diagram#

Fig. 268 .#
Equipment#
Baseball bat and “cradle” (see Figure 269A).
Meter stick.
Mathematical pendulum.
Rubber hammer.
Presentation#
The meterstick is suspended as a physical pendulum. The point of suspension is the percussion point when the stick is hit at about \(67 \mathrm{~cm}\) (see demonstration Percussion point. The distance of \(67 \mathrm{~cm}\) is also the reduced length of this pendulum (see demonstration Physical pendulum (1). This is quickly shown by suspending a “mathematical” pendulum close to the suspended stick (see the arrangement on the left side of Diagram) and making both swing: when the “mathematical” pendulum has a length of \(67 \mathrm{~cm}\), they will have the same period; swinging together, they stay together. The conclusion can be that when you hit the stick at the point of reduced length, the point of suspension will be the percussion point.
The baseballbat has a hole drilled in its shaft at the point between the two hands that would grasp the bat. In this hole a bar is stuck, extending on both sides. These ends rest on the flat surfaces of the “cradle” (see Figure 269A), so the bat can rock to and fro.
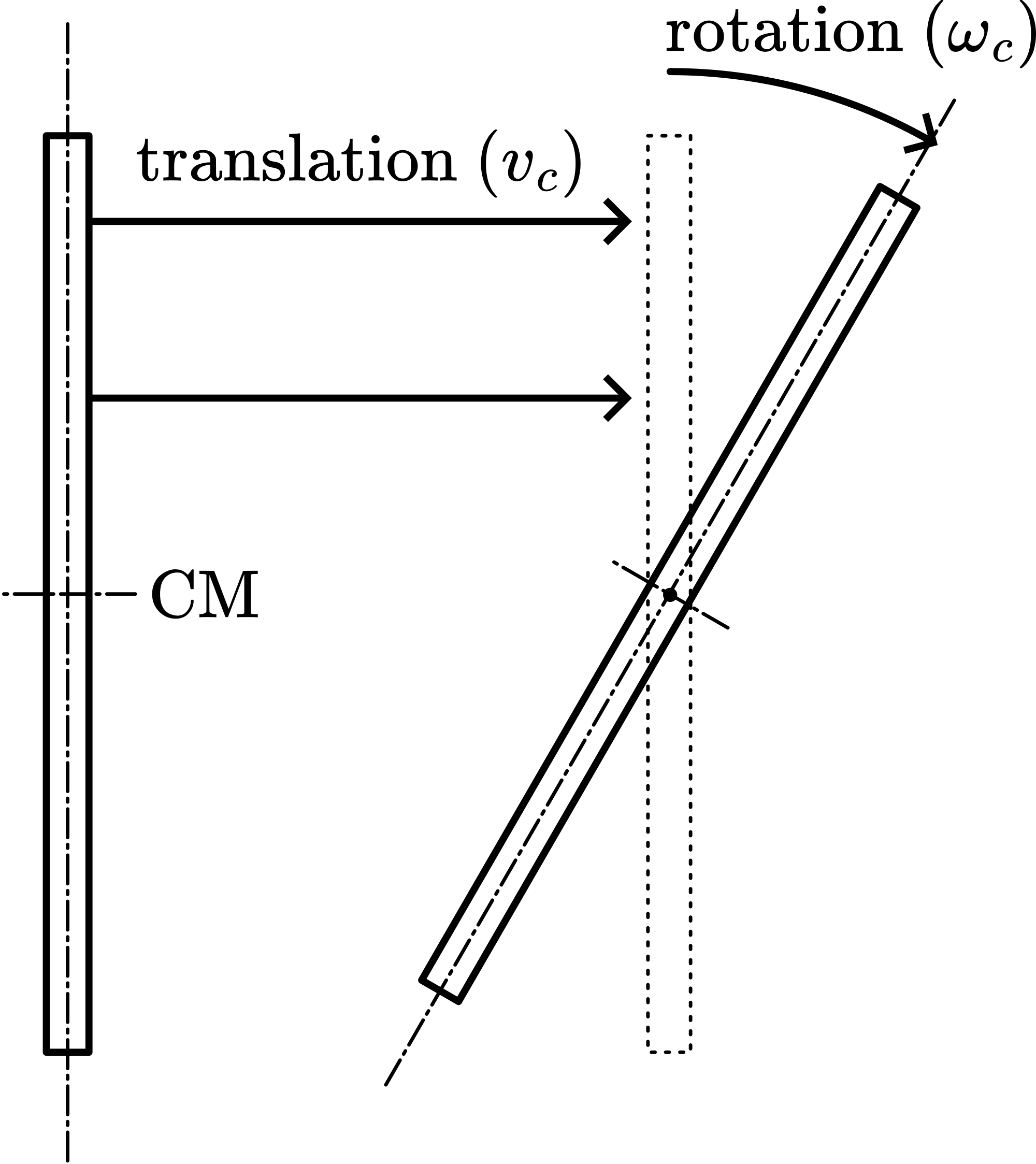
Fig. 269 .#
Using the rubber hammer, the bat is hit close to its point of suspension: The bat swings and on its horizontal surfaces of suspension it also displaces itself into the direction the hammer was hitting.
Then the hammer hits the bat at its lowest point. Again the bat swings, but now the displacement on the surface of suspension is into a direction opposite to the hitting hammer.
Conclusion will be that somewhere in between, the bat can be hit causing only a rotation at the suspension point. (By trial and error this point can be located.) We mount the mathematical pendulum close to the bat (see Figure 269 B) and increase its length until it swings with the same period as the free suspended bat does. Then we hit the bat at the point indicated by the bob of the mathematical pendulum, and the bat only rotates at the suspension point; there is no translation.
Explanation#
In the Explanation of the demonstration Physical pendulum (1), it is shown that the reduced length of a physical pendulum equals \(\frac{I_{c}}{\mathrm{~ms}}+c\). In the Explanation of the demonstration Percussion point it is shown that \(x=\frac{I_{c}}{m b}\), while the percussion point is \(\mathrm{b}+\mathrm{x}\) away from the point of hitting. Comparing both explanations, it is easy to see that \(\frac{I_{c}}{m c}+s=\frac{I_{c}}{m b}+b\) :
The distance to the percussion point is equal to the reduced length.
Remarks#
The flat surfaces of the cradle are covered with sandpaper and the extending shafts of the bat are fitted with a tight rubber hose. This is done to have just enough friction.
Use a water level to mount the cradle. That’s why we install the extra slanting shaft that is protruding backward (see Diagram).
The situation where the percussion point is at the point of suspension is not the situation for maximum energy transfer to the ball (see demonstration Sweet spot in this database).
In some literature not the point of pure rotation is called percussion point. Then that name is given to the point where the ball hits the bat and makes it rotate around the point of suspension without translation; so just the other way round.
Sources#
Borghouts, A.N., Inleiding in de Mechanica, pag. 182-183
Meiners, Harry F., Physics demonstration experiments, part I, pag. 355
Roest, R., Inleiding Mechanica, pag. 176-177
Young, H.D. and Freeman, R.A., University Physics, pag. 327-328
