11 Pulling the Rug

11 Pulling the Rug#

Aim#

To show a counterintuitive demonstration that can be explained using conservation of angular momentum.

Subjects#

  • 1Q40 (Conservation of Angular Momentum)

Diagram#

../../../../../_images/figure_099.png

Fig. 223 .#

Equipment#

  • Piece of tube (\(\varnothing=125 \mathrm{~mm}, l=120 \mathrm{~mm}\) ). We use a pvc coupling sleeve.

  • Two rubber bands, fixed around the ends of the tube.

  • Paper sheet. We use \(90 \times 25 \mathrm{~cm}^{2}\).

  • Air level.

  • Solid cylinder.

Presentation#

  • Accurately level the table. Place the tube on the sheet of paper and position a stick on the table to indicate the starting position of the tube.

    The sheet of paper is pulled horizontally out from under the tube. The observed movement of the tube is puzzling to the students, so the demonstration has to be repeated in order to make them describe exactly what they see:

    • At first the tube is at rest.

    • Pulling the sheet to the right makes the tube turn counter clockwise and there is a translation to the right (see Figure 224).

    • When the sheet leaves from under the tube, immediately the tube stops its rotation and translation!

../../../../../_images/figure_173.png

Fig. 224 .#

  • When a tube and a solid cylinder are placed side by side on the sheet of paper the distances traveled in the direction of the pull will differ from each other: the tube will travel farther than the solid cylinder!

Explanation#

  • When the sheet is pulled to the right, the tube wants to stay where it is due to its inertia. But due to friction the tube will slide along with the sheet. Seen from a point on the table this means a clockwise rotation. Yet, there is no torque applied to the tube, since the sheet is very thin! The only way not to violate conservation of angular momentum (which is zero all the time during this demonstration) means that the tube itself has to turn counter clockwise (see Figure 224).

  • The angular momentum due to the translation of the centre of mass of the object and due to the rotation of the object about its centre of mass must be equal in magnitude and opposite in direction.

  • When the tube leaves the sheet the only way for the tube to continue moving would mean that the two components of angular momentum should have the same direction. Since the net angular momentum is zero, movement is not possible any longer.

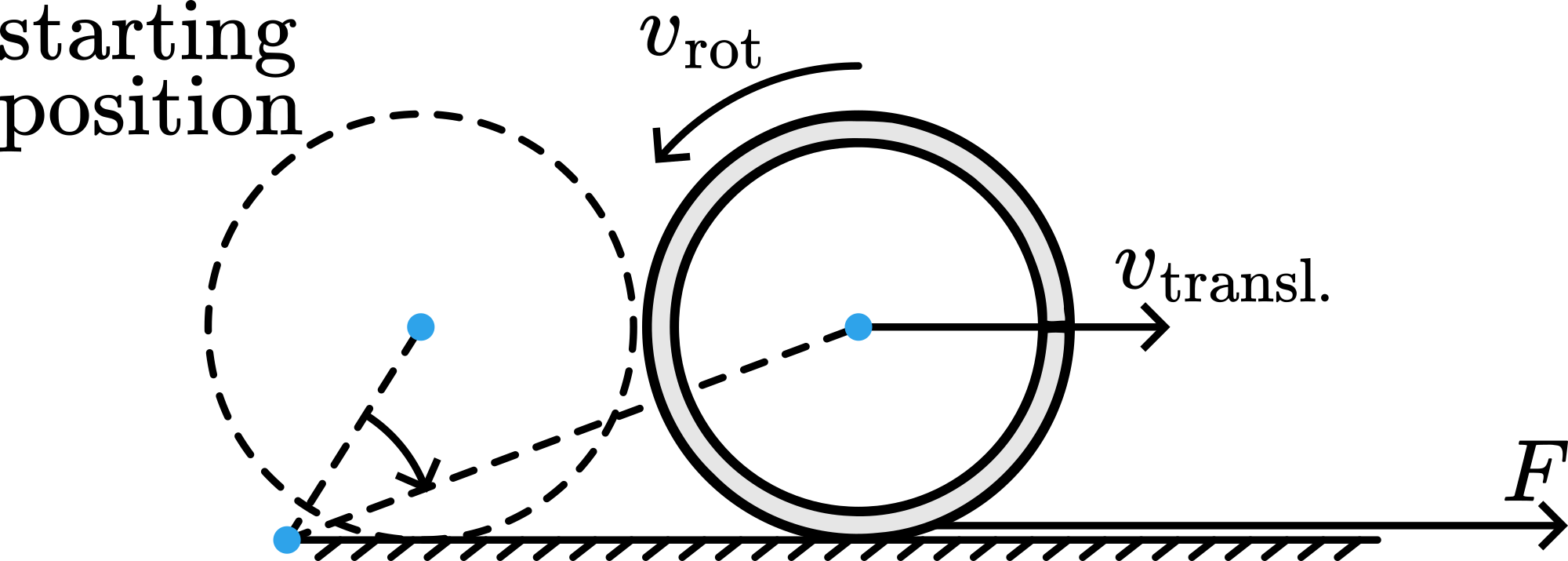
../../../../../_images/figure_231.png

Fig. 225 .#

  • The race between tube and solid cylinder seems to give a contrast with the results of Rolling downhill. But realizing that the tube has, relatively to its mass, a higher moment of inertia (ideal tube: \(M R^{2}\);solid cylinder: \(1 / 2 M R^{2}\) ) will give the insight that the mechanism is the same: The angular acceleration of the tube will be smaller than that of the solid cylinder and so the tube is taken further into the direction of translation. (Figure1 and 2 show that \(v_{\text {rot }}\) gives a displacement opposite to the direction of \(F\), so the lesser the object rotates the larger the displacement into the direction of \(F\) will be.)

Analysis will show that an ideal tube has a horizontal displacement \(D=d\) and a solid cylinder \(D=1 / 2 d\) (see Sources). So the (ideal) tube will be twice as far as the solid cylinder from their common starting point on the table.

Sources#

  • Roest, R., Inleiding Mechanica, pag. 181-182

  • The Physics Teacher, Vol.39, April2001, pag. 224-225

Contents