09 Pulling a Sliding Block

09 Pulling a Sliding Block#

Aim#

Showing the difference between static and kinetic friction

Subjects#

  • 1K20 (Friction)

Diagram#

../../../../../_images/figure_050.png

Fig. 119 .#

Equipment#

  • Wooden block

  • Pulley

  • String

  • Slotted masses

Presentation#

The slotted mass is made so heavy that the block just doesn’t move. Then you give a smash on the table and the block will start sliding and keep on sliding.

Explanation#

When the block just doesn’t move, it means that \(F_{f}\) is almost equal to \(F_{f, \max }=\mu_{\text {stat }} F_{n}\) (see Figure 120).

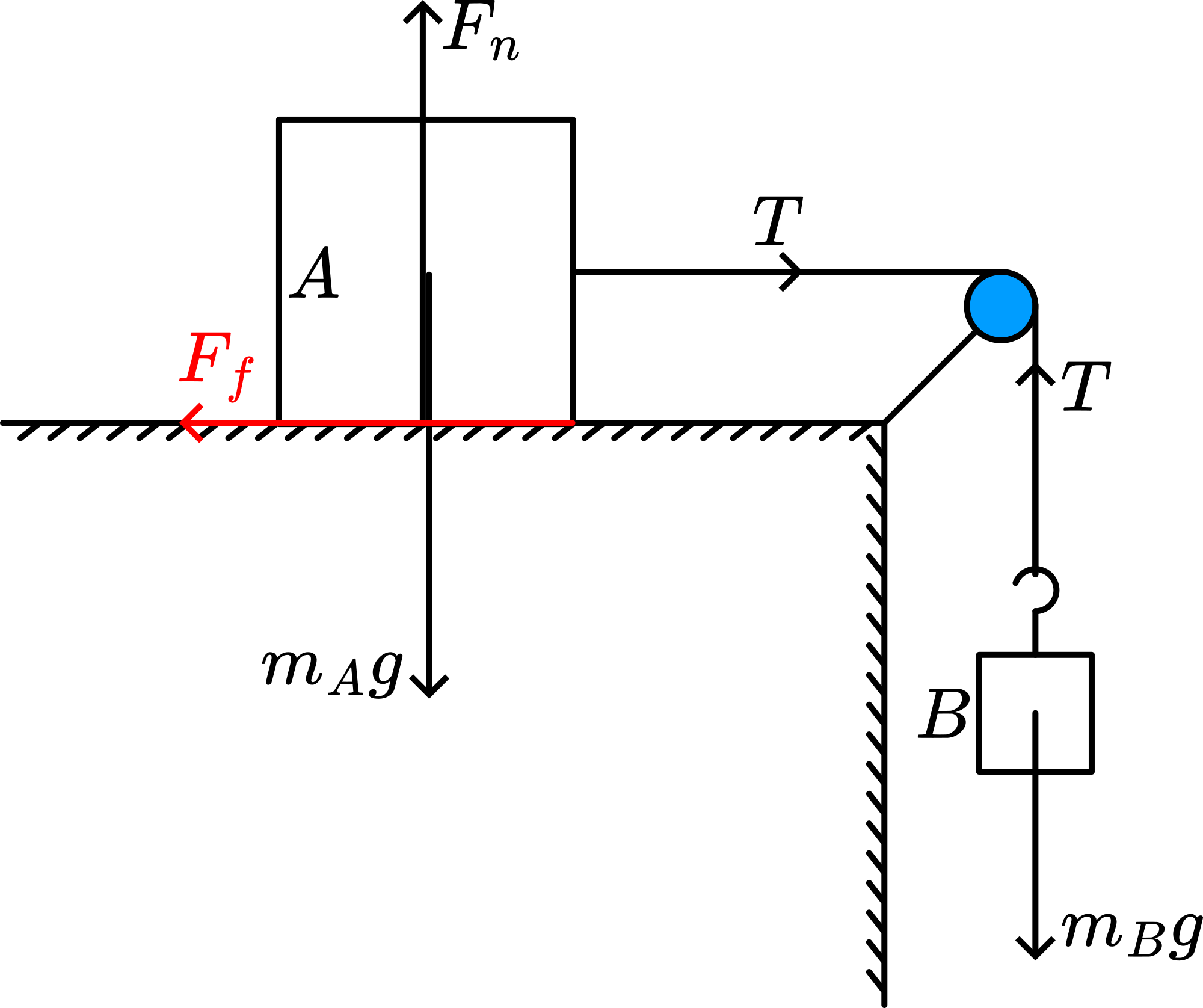
../../../../../_images/figure_139.png

Fig. 120 .#

A smash on the table means that the block is released from the table for a short moment (at least temporarily \(F_{n}\) will be much smaller than \(m_{A} g\) ) so A and B start moving. Since \(A\) and \(B\) continue to move, it means that \(\mu_{k i n} F_{n}\left(=m_{B} g\right)\) is lower than \(\mu_{\text {stat }} F_{n}\).

Remarks#

  • The ring for fixing the string can be moved vertically in order to maintain the pulling string horizontal when the block is moving.

  • A wetted bottom of the block makes this demonstration somewhat easier.

Sources#

  • Roest, R., Inleiding Mechanica, pag. 63

Contents