07 Dumb-Bell

07 Dumb-Bell#

Aim#

To show that change in direction of angular momentum needs a torque.

Subjects#

  • 1Q40 (Conservation of Angular Momentum) 1Q60 (Rotational Stability)

Diagram#

../../../../../_images/figure_095.png

Fig. 217 .#

Equipment#

  • Dumbbell pivoted on a support at a non-symmetry axis through the center of mass.

  • Frame in order to lift off the dumbbell from the support

Presentation#

The dumbbell is placed on top of the support. A thread is fixed to the center of mass and thrown over the top of the frame and hold slack, away from the dumbbell. The dumbbell is given a rotation by hand. Make the students observe that the two masses of the rotating dumbbell describe two horizontal circles (Figure 218a).

../../../../../_images/figure_172.png

Fig. 218 .#

Lift the dumbbell from its support. Almost immediately it can be seen that now the rotation of the dumbbell takes place in one slanting plane (Figure 218b).

Before lift-off it can be seen that while the dumbbell rotates, the vertical support shaft oscillates/shakes/wobbles strongly and yet it is a thick and strong steel shaft!

Explanation#

The dumbbell-shaped object rotates about a non-symmetry axis through the center of mass O. Figure 219a shows the angular momentum vector of the rotating dumbbell relative to \(\mathrm{O}\) at the instant drawn and while the dumbbell rotates the angular momentum vector describes a cone. So the angular momentum changes direction continuously. To do this a torque is needed. The ballbearing support at O gives that torque: A centripetal force \(F_{c}\) is needed to move \(m\) around in a circle (see Figure 219b). This needs a torque \(\vec{F}_{c} \times \vec{r}\). (Also \(\vec{M}=\frac{d \vec{L}}{d t}\) gives this result.)

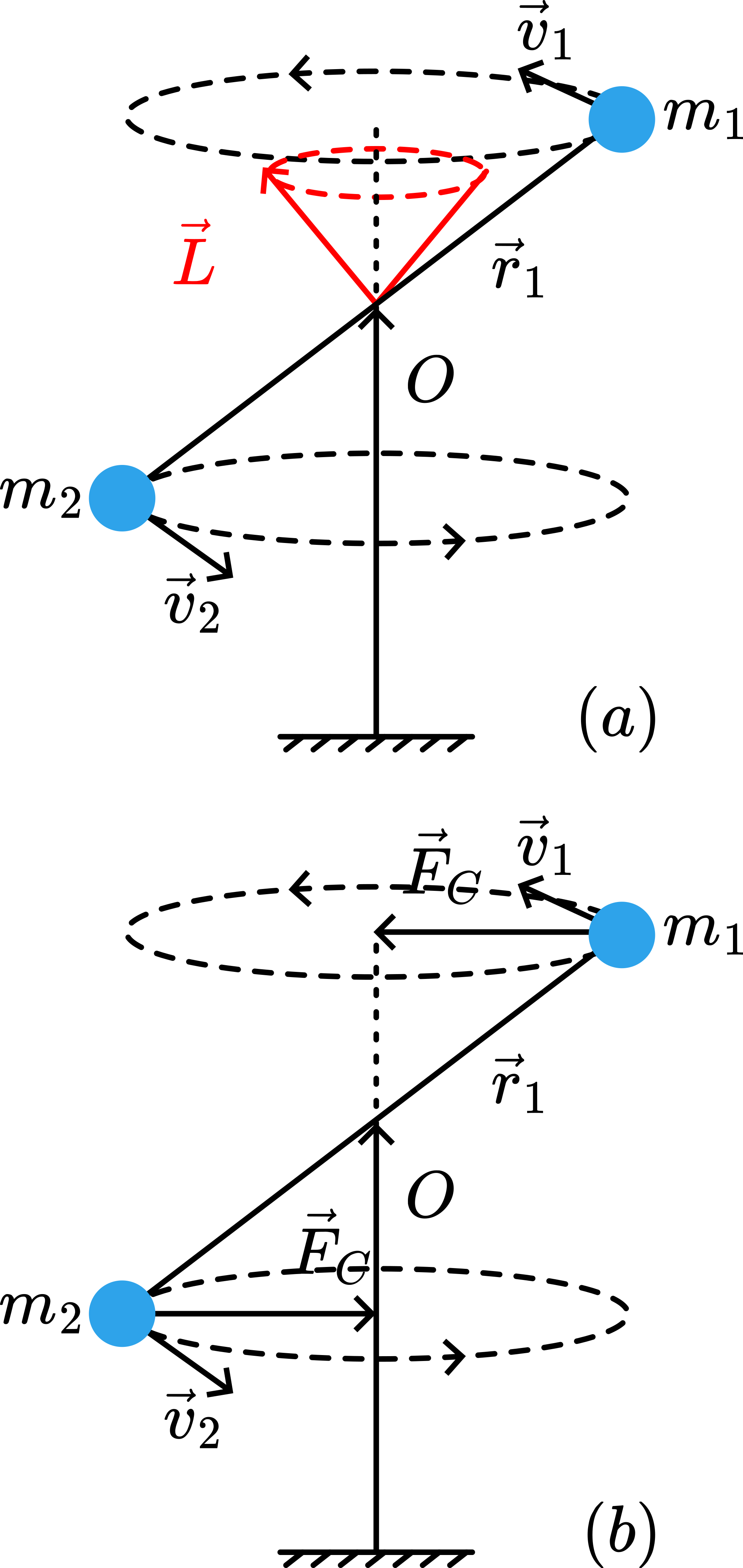
../../../../../_images/figure_230.png

Fig. 219 .#

This torque also makes the support shaft wobble. The dumbbell needs to rotate in such a way as the direction of \(\vec{L}\) dictates at the moment of lift-off.

Remarks#

  • The wobbling of the support shaft can also be described in terms of dynamical unbalance: The angular momentum ( \(\vec{L}\) ) and the angular velocity \((\vec{\omega})\) are not parallel.

Sources#

  • Alonso, M/Finn, E. J., Fundamentele Natuurkunde, part 1, Mechanica, pag. 215-217

  • Borghouts, A.N., Inleiding in de Mechanica, pag. 221-223

  • PSSC, College Physics, pag. 352-355 and 366-367

  • Roest, R., Inleiding Mechanica, pag. 212-213

  • Giancoli, D.G., Physics for scientists and engineers with modern physics, pag. 287

Contents