04 Percussionpoint (1)#
Aim#
To show the behavior of a stick to a short impulse.
Subjects#
1Q60 (Rotational Stability)
Diagram#
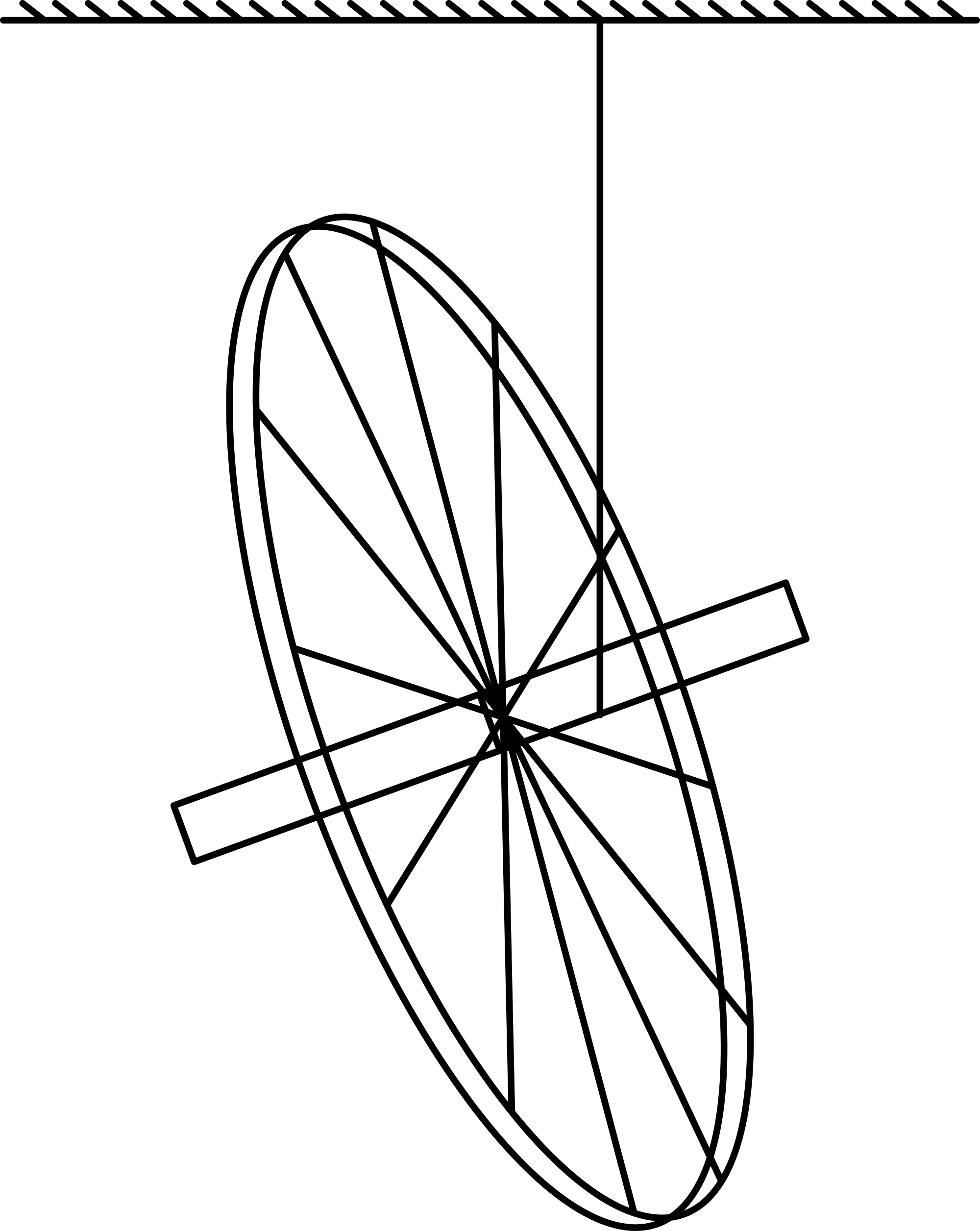
Fig. 265 .#
Equipment#
Platform with grid, used as reference.
Ruler, \(1 \mathrm{~m}\).
Stick.
Presentation#
Place the ruler with its centerline on the thick centerline of the grid (see Diagram). With the stick you give a short blow to the center of the stick (a movement like you are playing pool-billiards). There will result a translation of the stick.
Again place the ruler with its centerline on the grid. With the stick you give a short blow to the ruler e.g. at \(60 \mathrm{~cm}\). There will result a translation and rotation of the stick.
With the stick you give a short blow to the ruler at \(100 \mathrm{~cm}\). There will result a translation and rotation of the stick. Special is that it rotates around the point of \(33 \mathrm{~cm}\) on the ruler.
With the stick you give a short blow to the ruler at \(67 \mathrm{~cm}\). There will result a translation and rotation of the stick. Special is that it rotates around the beginning of the stick.
The point, around which the stick rotates is called “percussion point”. In point 3 and -4 , this point is on the stick; in point 2 it is outside the stick.
Explanation#
Due to the short blow, the ruler performs a movement that can be considered as consisting of two movements: a translation and rotation around its center of mass \(\mathrm{~CM}\) (see Figure 266).

Fig. 266 .#
During the short blow force acts on the ruler. The total momentum of this force is \(\int F dt=p\). The ruler gets a speed \(v_{c}\), so the momentum of the ruler is \(m v_{c}\). This makes \(v_{c}=p / m\).
Relative to \(\mathrm{CM}\) the ruler has also an angular momentum \(I_{c} \omega_{c}=b p\) (see Figure 267). So \(\omega_{c}=b p / I_{c}\) On one side of \(\mathrm{CM}, v_{c}\) and \(\omega_{c}\) have the same direction; on the other side \(v_{c}\) and \(\omega_{c}\) are opposite to each other. Looking at point A: \(v_{A}=v_{c}-\omega_{c} x\). When point A remains at rest after the blow (A is then the so-called percussion point) then \(0=v_{c}-\omega_{c} x\). This happens at \(x=\frac{v_{c}}{\omega_{c}}=\frac{p / m}{b p / I_{c}}=\frac{I_{c}}{m b}\). For this ruler: \(I_{c}=1 / 12 m l^{2}\), making \(x=\frac{1}{12} \frac{l^{2}}{b}\).
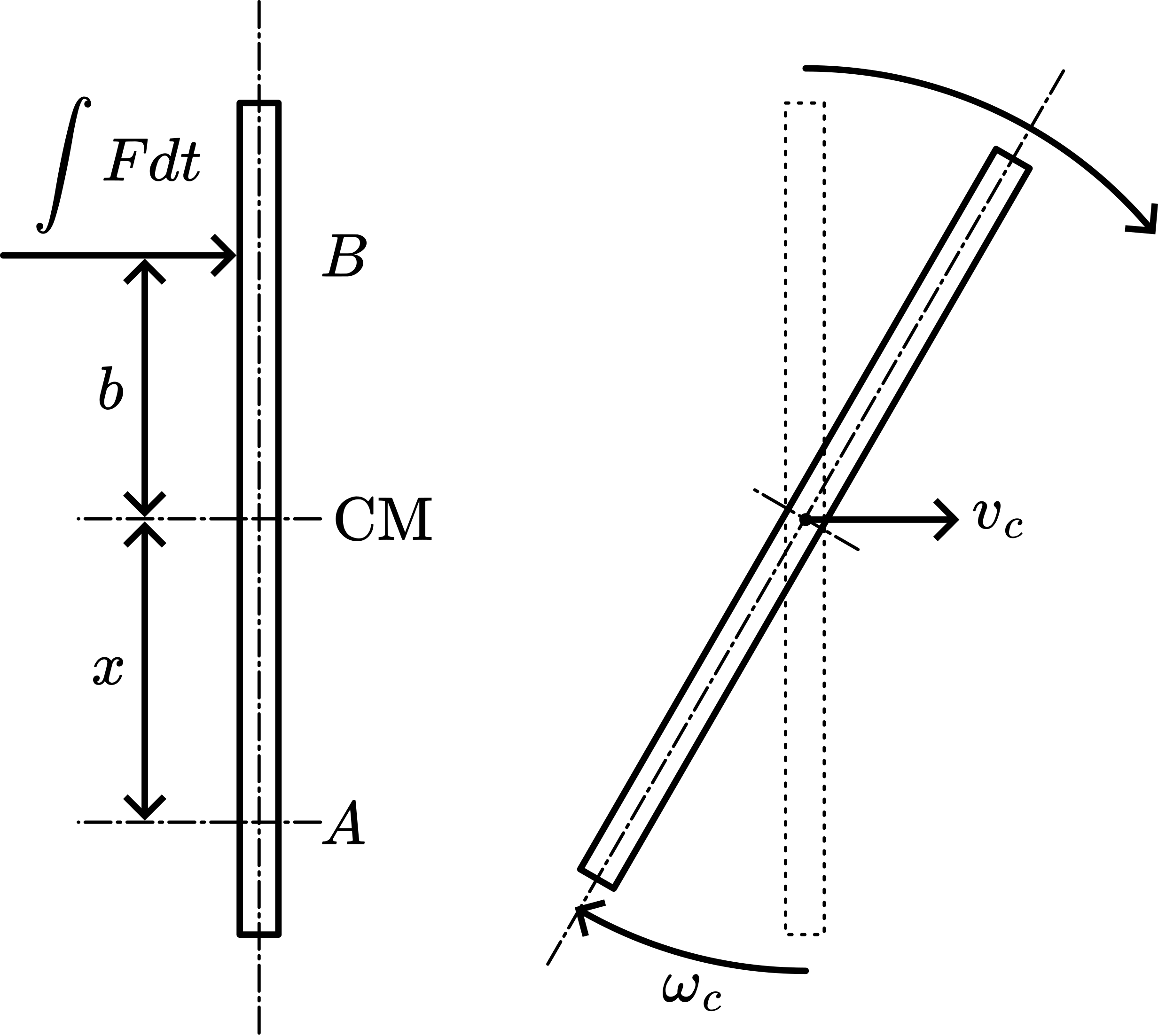
Fig. 267 .#
Applying this to the different situations of the Presentation shows the observed percussion points: in PresentationXX point 1 \((b=0)\), point 3 \((b=.5 \mathrm{~m})\) and point 4 \((b=.17 \mathrm{~m})\). In PresentationXX \((b=.1 \mathrm{~m})\), the percussion point is outside the ruler \((x=.83 \mathrm{~m})\).
Remarks#
Playing billiards with a stick instead with a ball needs practice!
Sources#
Borghouts, A.N., Inleiding in de Mechanica, pag. 182-183
Roest, R., Inleiding Mechanica, pag. 172-173 and 176-177
