01 Force on Electrons in a Magnetic Field (1)#
Aim#
To show the effect of a magnetic field on a sweeping beam of electrons (oscilloscope).
Subjects#
5H30 (Force on Moving Charges)
Diagram#
Fig. 505 .#
Equipment#
Oscilloscope, cover removed (see Diagram).
2 Signal generators.
Small bar magnet.
Video camera and projector to present the screen of the oscilloscope to a large audience.
Safety#
The power supply of the oscilloscope tube has a dangerous high tension. So, take care when the cover is removed. The parts with the high tension are clearly labelled. Nevertheless, take care when doing this demonstration!
Presentation#
Preparation:#
Remove the cover of the oscilloscope and notice the high tension labels (see: Safety).
Presentation#
Switch on the oscilloscope and set its time-base so a stable horizontal line appears on the screen (see Diagram). Explain to the students that a beam of electrons is moving from the back to the front side (fluorescent screen) of the oscilloscope, where it appears as a line.
1.#
Ask the students what will happen to that line when you approach the oscilloscope tube with a North pole coming from the left side of the oscilloscope. As a comment to their answers, show that the end of the line goes downward (see Figure 506B).

Fig. 506 .#
Lorentz force and right hand rule can be discussed properly now. As an illustration approach the side of the oscilloscope also with the South pole and see the effect.
2.#
Next step is to approach the front of the oscilloscope with the North pole of the bar magnet. Ask the students what will happen to the horizontal line.
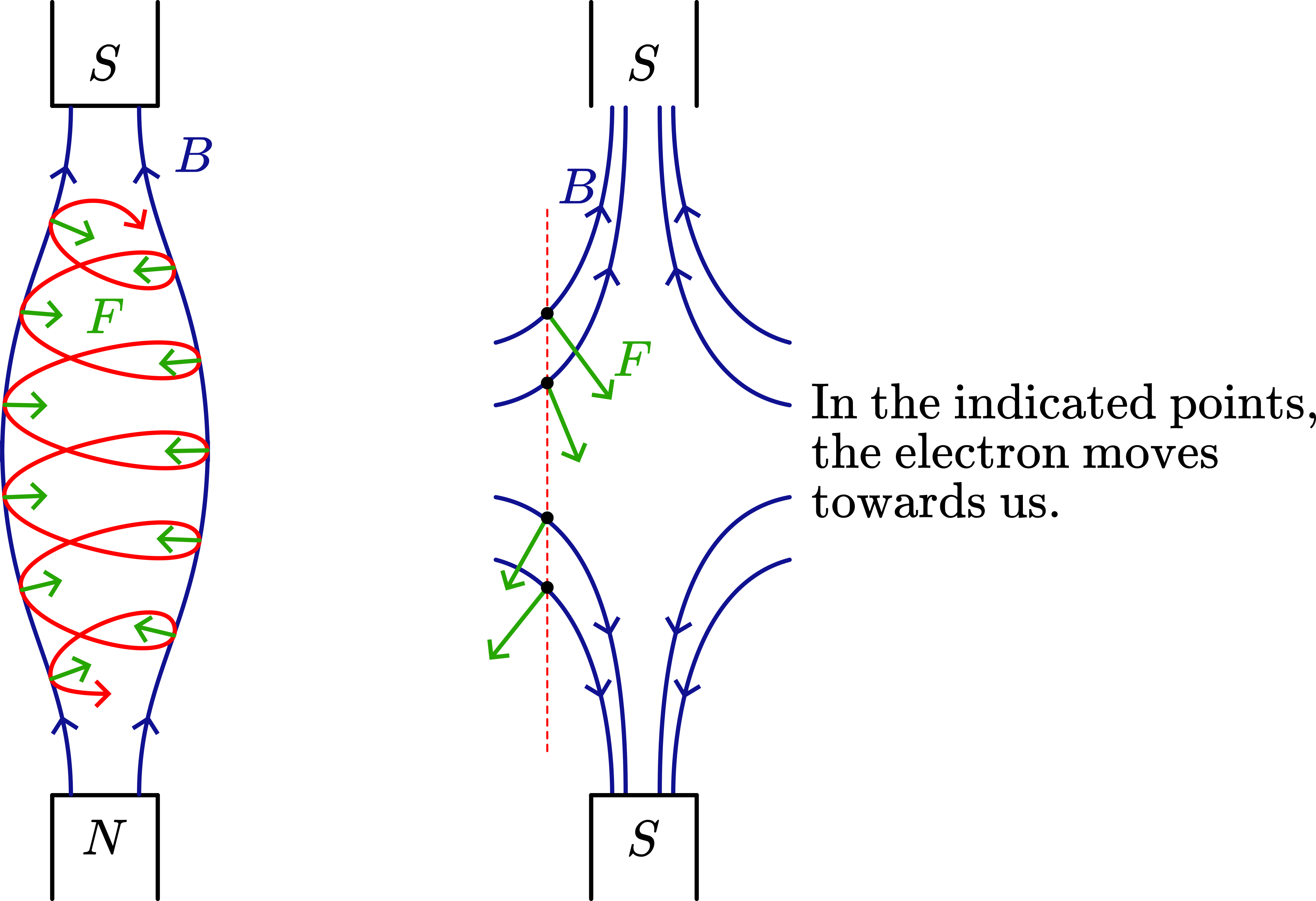
Fig. 507 .#
Then approach the front of the oscilloscope screen with the bar magnet. Figure 507B shows the effect on that line. Observe that in het centre of the bar magnet there is no displacement. A more detailed discussion with the students is needed to explain what is happening on the right and left (see Explanation).
3.#
The next challenging question is: “What will happen to the horizontal line when I approach it with the bar magnet parallel to that line?” After their answers do the demonstration (see Figure 508B).

Fig. 508 .#
Observe that above the magnet the line has risen above the original horizontal line, and at the left and right of the bar magnet that the line has descended below the original horizontal line.
4.#
The oscilloscope is connected to the two signal generators and used as an \(x-y\) scope (see Figure 509B).

Fig. 509 .#
The two signal generators are set such that a filled square appears on the screen ( \(\mathrm{a}\) Lissajous figure with a random ratio between the two frequencies).
Slowly approaching this square with a North pole makes visible that the electron beam spirals around the magnetic field lines (see Figure 510B), and that the beam even makes

Fig. 510 .#
a focus (Figure 510BF and G$ ): the magnetic field can act on a beam of electrons in a way like an optical lens acts on light beams: the magnetic field acts as a lens on the electron-beam.
Explanation#
The force ( \(F\) ) on a moving ( \(v\) ) charge \((\mathrm{q})\) in a magnetic field \((B)\) is expressed as \(\vec{F}=q \stackrel{\rightharpoonup}{v} \times \vec{B}\) (Lorentz force).
1.#
In order to find the right direction of the take into account that the charge \(q\) is negative! (In this introductive demonstration and its explanation it is just enough to talk about the magnetic field going into one direction, perpendicular to the electron beam.)
2. and 3.#
Considering the direction of the force in the Figure 507B and Figure 508B, again keep in mind that charge \(q\) is negative! Key to the force in these drawings is that the angle between \(v\) and \(B\) is not \(0^{\circ}\) (see Figure 511B).
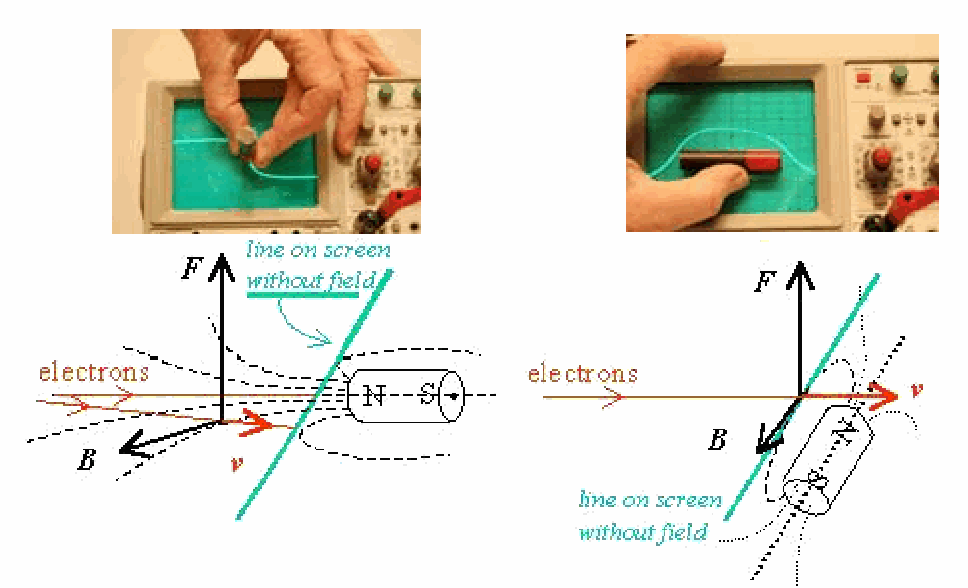
Fig. 511 .#
In Figure 507B it can be observed also that the central electrons are not deflected. This is right, because for these electrons (and only for these electrons) \(\stackrel{\rightharpoonup}{V} \times \vec{B}=0\).
4.#
Figure \(5 \mathrm{~B}\) and \(5 \mathrm{C}\) show clearly a rotation to the right. This is the same rotation that is already observed in the demonstration of Figure 507B: there it was only a line; now the whole square (electron beam) can be seen rotating. (During the whole demonstration the rotations remains clearly visible.) The rotation becomes a spiral, because close to the magnet the magnetic field is so much stronger than farther away from the magnet. (Many books show these spirals, e.g. Giancoli, pag. 694; see SourcesXX.) That focussing occurs illustrates that with electron beams we can create a microscope (electron microscope).
Remarks#
Also the picture on a TV- or monitor screen can be distorted by using magnets, but take care, the distortion might be irreparable!
Also see the demonstration Force on electrons in a magnetic field in this database.
Sources#
Biezeveld, H. and Mathot, L., Scoop, Natuurkunde voor de bovenbouw, part 4/5 vwo, pag. 211
Mansfield, M and O’Sullivan, C., Understanding physics, pag. 497-498
Young, H.D. and Freeman, R.A., University Physics, pag. 867-868
Giancoli, D.G., Physics for scientists and engineers with modern physics, pag. 692
